치춘짱베리굿나이스
[백준] 3053 본문
택시 기하학
문제
19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.
택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.
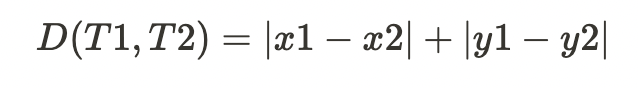
두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.
따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.
원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합
반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 반지름 R이 주어진다. R은 10,000보다 작거나 같은 자연수이다.
출력
첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.
풀이
const taxi = () => {
let input = parseInt(
require("fs").readFileSync("/dev/stdin").toString().trim()
);
console.log(`${input * input * Math.PI}\n${input * input * 2}`);
};
taxi();반성회
원의 정의를 동그라미 가 아니라 평면 상의 어떤 점에서 거리가 일정한 점들의 집합 이라는 정확한 정의로 생각해보면 택시 기하학에서의 원은 동그라미 모양이 아니라는 것을 알 수 있다 (마름모 모양이더라)
기준점에서 반지름*2 만큼의 가로세로 길이를 가진 마름모이므로
(반지름 * 2 * 반지름 * 2) / 2
=== (반지름 * 반지름 * 2)와 같이 계산하면 된다
'Javascript + Typescript > 자바스크립트로 알고리즘풀기' 카테고리의 다른 글
| [백준] 2750 (0) | 2022.02.13 |
|---|---|
| [백준] 1002 (0) | 2022.02.13 |
| [백준] 2447 (0) | 2022.02.13 |
| [백준] 10822 (0) | 2022.02.13 |
| [백준] 17608 (0) | 2022.02.13 |
Comments

