C C++/알고리즘풀이

[백준] 9251

치춘 2023. 8. 9. 22:47

LCS

문제

LCS(Longest Common Subsequence, 최장 공통 부분 수열)문제는 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제이다.

예를 들어, ACAYKP와 CAPCAK의 LCS는 ACAK가 된다.

입력

첫째 줄과 둘째 줄에 두 문자열이 주어진다. 문자열은 알파벳 대문자로만 이루어져 있으며, 최대 1000글자로 이루어져 있다.

출력

첫째 줄에 입력으로 주어진 두 문자열의 LCS의 길이를 출력한다.

풀이

#include <iostream>
#include <string>
#include <algorithm>

int arr[1002][1002] = {0};

void printArr(int aLen, int bLen) {
    for (int i = 0; i <= aLen; i++) {
        for (int j = 0; j <= bLen; j++) {
            std::cout << arr[i][j] << " ";
        }
        std::cout << "\n";
    }
}

int main(void) {
    std::string a, b;
    int aLen, bLen;

    std::cin >> a >> b;

    aLen = a.length();
    bLen = b.length();

    for (int i = 1; i <= aLen; i++) {
        for (int j = 1; j <= bLen; j++) {
            if (a[i - 1] == b[j - 1]) {
                arr[i][j] = arr[i - 1][j - 1] + 1;
            } else {
                arr[i][j] = std::max(arr[i - 1][j], arr[i][j - 1]);
            }
        }
    }

    // printArr(aLen, bLen);
    std::cout << arr[aLen][bLen];
}

반성회

https://velog.io/@emplam27/알고리즘-그림으로-알아보는-LCS-알고리즘-Longest-Common-Substring와-Longest-Common-Subsequence

 

[알고리즘] 그림으로 알아보는 LCS 알고리즘 - Longest Common Substring와 Longest Common Subsequence

LCS는 주로 최장 공통 부분수열(Longest Common Subsequence)을 말합니다만, 최장 공통 문자열(Longest Common Substring)을 말하기도 합니다.

velog.io

이 블로그에 설명이 정말 잘 되어 있다… 감사합니다

어떻게 풀어야 할지 감도 못 잡고 있었는데 블로그 보고 이해함

기본 내용

ACAYKP
CAPCAK

두 문자열을 이용하여 최장 부분 문자열을 뜯어온다고 가정하자

 

첫 번째 줄은 0으로 초기화한다

아래에서도 나오겠지만 i - 1 인덱스에 접근하는 경우가 생기므로 음수 인덱스 접근 방지를 위해 채워주는 느낌이라고 생각하면 될 것

 

첫 행부터 채워나간다

  • A와 C가 만나는 부분 → A와 C의 비교 → LCS 없음
  • C와 C가 만나는 부분 → AC와 C의 비교 → LCS: C
  • A와 C가 만나는 부분 → ACA와 C의 비교 → LCS: C
  • Y와 C가 만나는 부분 → ACAY와 C의 비교 → LCS: C
  • K와 C가 만나는 부분 → ACAYK와 C의 비교 → LCS: C
  • P와 C가 만나는 부분 → ACAYKP와 C의 비교 → LCS: C

  • A와 A가 만나는 부분 → A와 CA의 비교 → LCS: A
  • C와 A가 만나는 부분 → AC와 CA의 비교 → LCS: C 또는 A
  • A와 A가 만나는 부분 → ACA와 CA의 비교 → LCS: CA
    • 이때 길이는 각각의 이전 문자열이었던 AC와 C의 LCS에서 1을 더한 값
  • Y와 A가 만나는 부분 → ACAY와 CA의 비교 → LCS: CA
  • K와 A가 만나는 부분 → ACAYK와 CA의 비교 → LCS: CA
  • P와 A가 만나는 부분 → ACAYKP와 CA의 비교 → LCS: CA

부분 문자열이므로 LCS는 더 큰 값이 나오지 않는 이상 이전 값이 유지된다

 

 

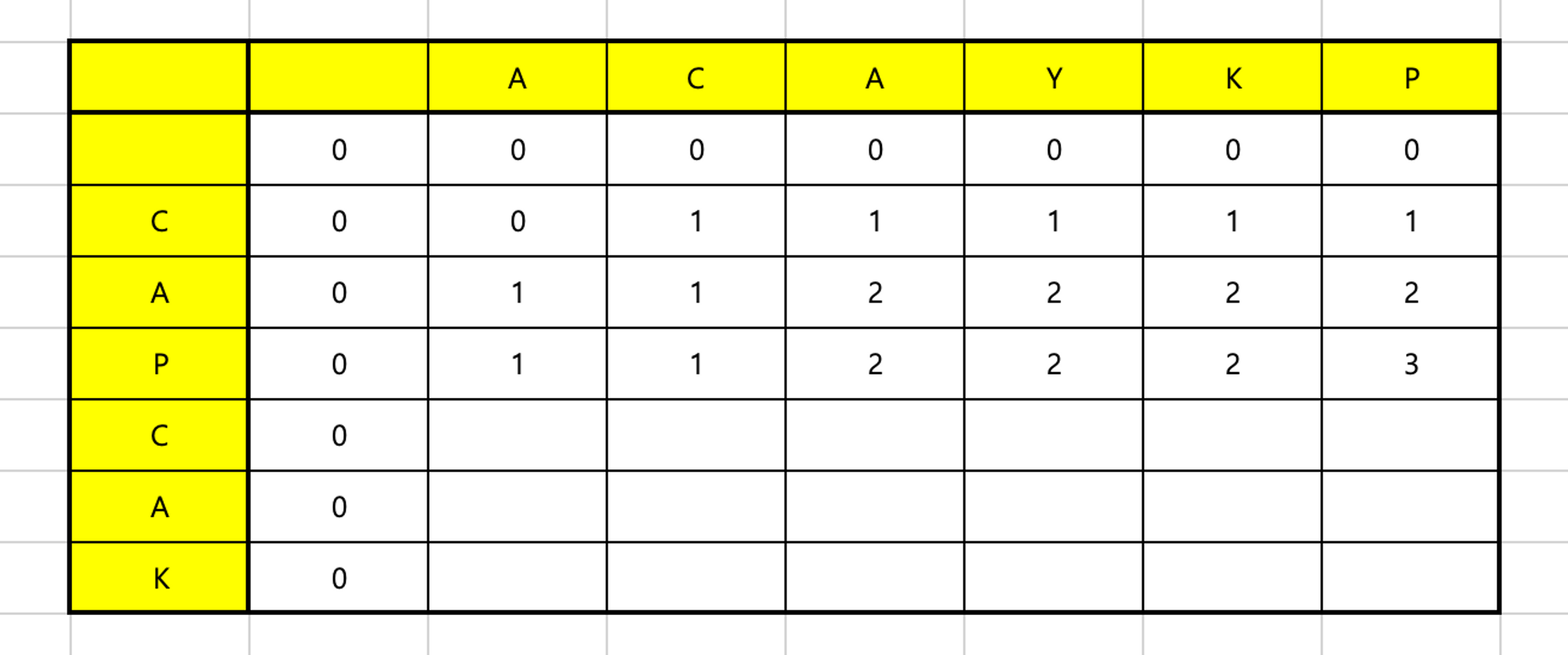
  • A와 P가 만나는 부분 → A와 CAP의 비교 → LCS: A
  • C와 P가 만나는 부분 → AC와 CAP의 비교 → LCS: C 또는 A
  • A와 P가 만나는 부분 → ACA와 CAP의 비교 → LCS: CA
  • Y와 P가 만나는 부분 → ACAY와 CAP의 비교 → LCS: CA
  • K와 P가 만나는 부분 → ACAYK와 CAP의 비교 → LCS: CA
  • P와 P가 만나는 부분 → ACAYKP와 CAP의 비교 → LCS: CAP
    • 이때 길이는 각각의 이전 문자열이었던 ACAYK와 CA의 LCS에서 1을 더한 값

 

  • A와 C가 만나는 부분 → A와 CAPC의 비교 → LCS: A
  • C와 C가 만나는 부분 → AC와 CAPC의 비교 → LCS: AC
  • A와 C가 만나는 부분 → ACA와 CAPC의 비교 → LCS: AC 또는 CA
  • Y와 C가 만나는 부분 → ACAY와 CAPC의 비교 → LCS: AC 또는 CA
  • K와 C가 만나는 부분 → ACAYK와 CAPC의 비교 → LCS: AC 또는 CA
  • P와 C가 만나는 부분 → ACAYKP와 CAPC의 비교 → LCS: CAP

  • A와 A가 만나는 부분 → A와 CAPCA의 비교 → LCS: A
  • C와 A가 만나는 부분 → AC와 CAPCA의 비교 → LCS: AC
  • A와 A가 만나는 부분 → ACA와 CAPCA의 비교 → LCS: ACA
    • 이때 길이는 각각의 이전 문자열이었던 AC와 CAPC의 LCS에서 1을 더한 값
  • Y와 A가 만나는 부분 → ACAY와 CAPCA의 비교 → LCS: ACA
  • K와 A가 만나는 부분 → ACAYK와 CAPCA의 비교 → LCS: ACA
  • P와 A가 만나는 부분 → ACAYKP와 CAPCA의 비교 → LCS: ACA 또는 CAP

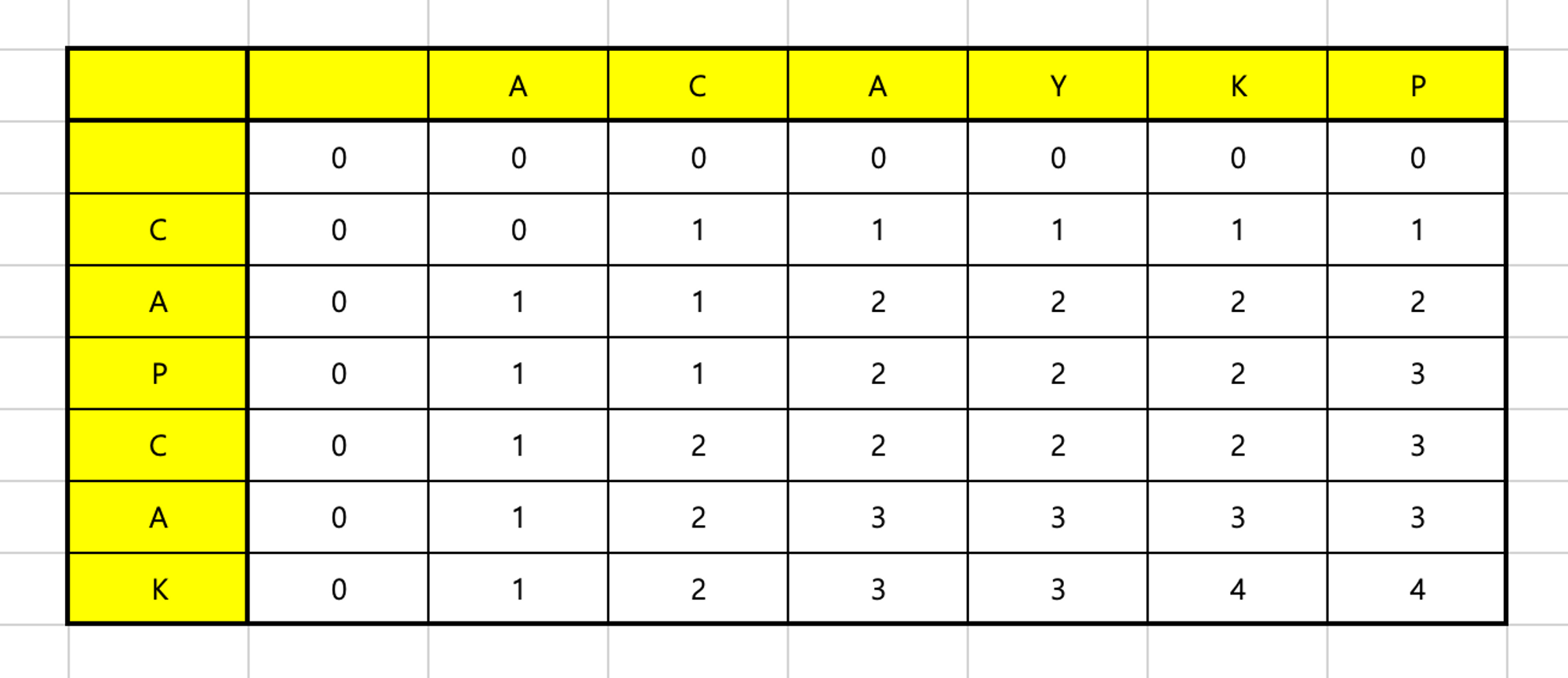
  • A와 K가 만나는 부분 → A와 CAPCAK의 비교 → LCS: A
  • C와 K가 만나는 부분 → AC와 CAPCAK의 비교 → LCS: AC
  • A와 K가 만나는 부분 → ACA와 CAPCAK의 비교 → LCS: ACA
  • Y와 K가 만나는 부분 → ACAY와 CAPCAK의 비교 → LCS: ACA
  • K와 K가 만나는 부분 → ACAYK와 CAPCAK의 비교 → LCS: ACAK
    • 이때 길이는 각각의 이전 문자열이었던 ACAY와 CAPCA의 LCS에서 1을 더한 값
  • P와 K가 만나는 부분 → ACAYKP와 CAPCAK의 비교 → LCS: ACAK
문자열 a (ACAYKP) 의 인덱스: i
문자열 b (CAPCAK) 의 인덱스: j 라고 가정
위 표의 배열은 arr이다

여기서 규칙이 2개가 등장하는데,

  • 같은 문자를 만날 경우 (a[i] == b[j]), 각각의 이전 문자열의 LCS에서 1 증가한 값을 갖는다
  • 오른쪽 아래 대각선으로 1 증가한다는 의미
    • arr[i][j] = arr[i - 1][j - 1] + 1
  • 다른 문자의 경우, 각각의 두 이전 문자열의 LCS 중 큰 값을 이어받는다
    • arr[i][j] = max(arr[i - 1][j], arr[i][j - 1])

문제가 됐던 코드

for (int i = 0; i < aLen; i++) { // 여기서 0으로 초기화하는 부분
    for (int j = 0; j < bLen; j++) { // 여기서 0으로 초기화하는 부분
        if (a[i] == b[j]) {
            arr[i][j] = arr[i - 1][j - 1] + 1; // 음수 인덱싱 되는 부분
        } else {
            arr[i][j] = std::max(arr[i - 1][j], arr[i][j - 1]); // 음수 인덱싱 되는 부분
        }
    }
}

계속 틀렸습니다가 나왔는데 인덱싱 문제였다

C에서는 배열에 음수 인덱스로 접근하면 undefined behavior이라 운이 좋으면 오류 없이 잘 넘어갈 수도 있지만 잘못 걸리면 오류가 발생할 수도 있다는 것

저작자표시 (새창열림)